Skip to main content

Section 2.3 Venn Diagrams

To visualize the interaction of sets, John Venn in 1880 thought to use overlapping circles, building on a similar idea used by Leonhard Euler in the 18th century. These illustrations now called Venn Diagrams.

Definition 2.3.1. Venn Diagrams.

A Venn diagram represents each set by a circle, usually drawn inside of a containing box representing the universal set. Overlapping areas indicate elements common to both sets.

Basic Venn diagrams can illustrate the interaction of two or three sets.

Example 2.3.2.

Create Venn diagrams to illustrate

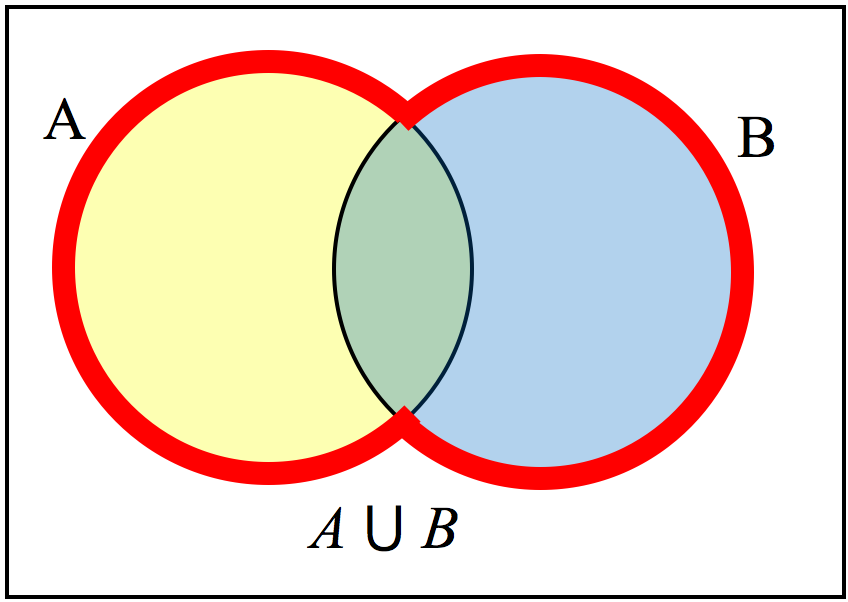
  1. \(\displaystyle A \cup B\)

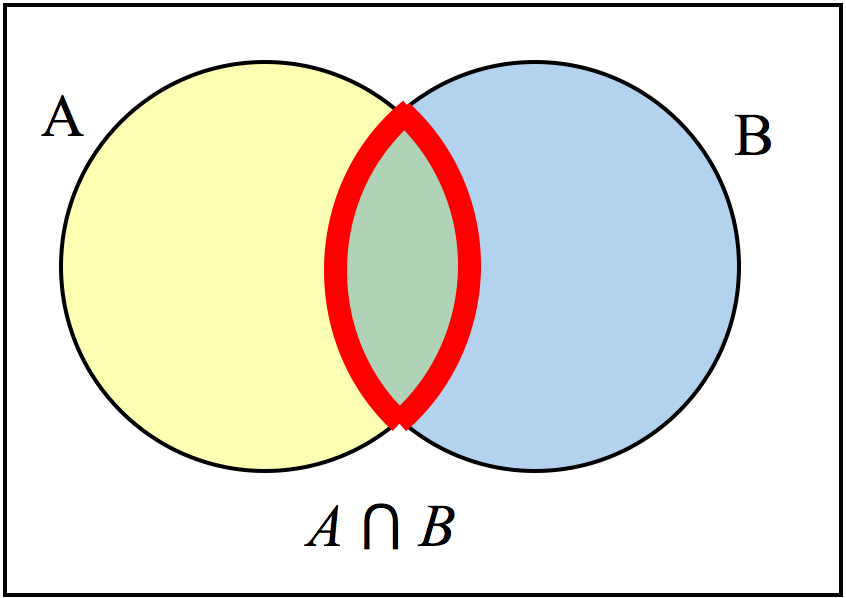
  2. \(\displaystyle A \cap B\)

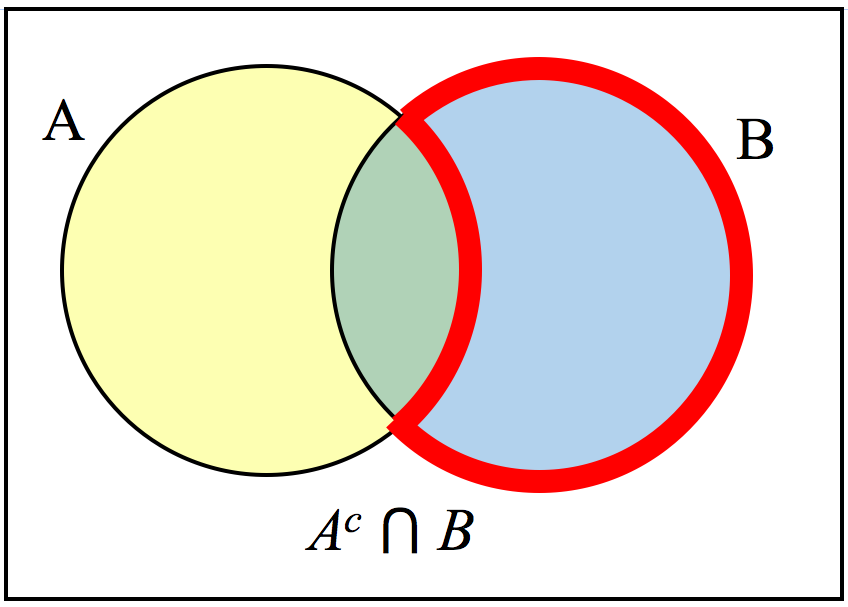
  3. \(\displaystyle A^C \cap B\)

Solution.

  1. \(A \cup B\) contains all elements in either set.

    The union of two sets contains everything in either set.

  2. \(A \cap B\) contains only those elements in both sets - in the overlap of the circles.

    The intersection of two sets contains the region in both sets--where they overlap.

  3. \(A^C\) will contain all elements not in the set A. \(A^C \cap B\) will contain the elements in set B that are not in set A.

    The intersection of elements that are not in set A and are in set B is the region in set B that is not inside of set A.
Example 2.3.3.

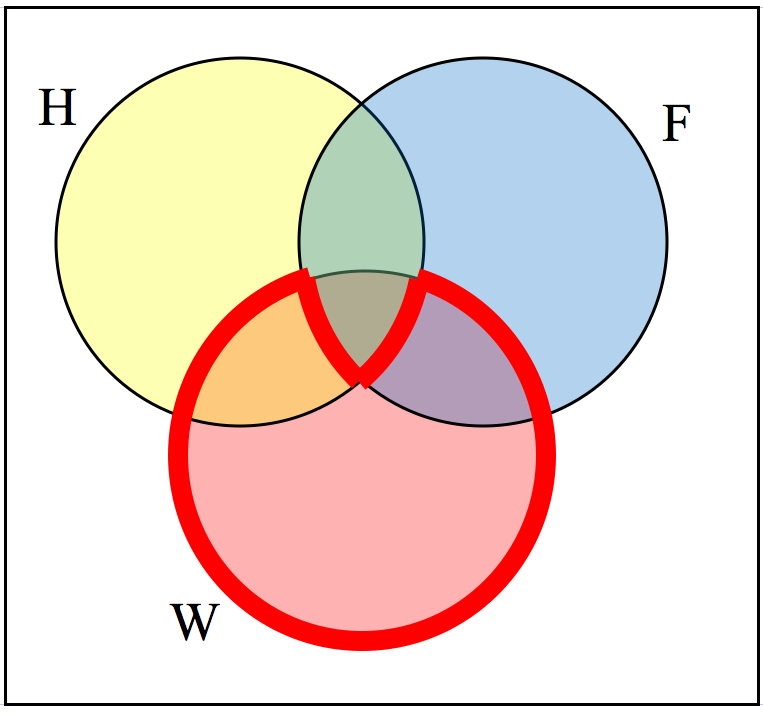
Use a Venn diagram to illustrate \(\left( H \cap F\right)^C \cap W\)

Solution.

We’ll start by identifying everything in the set \(H \cap F\)

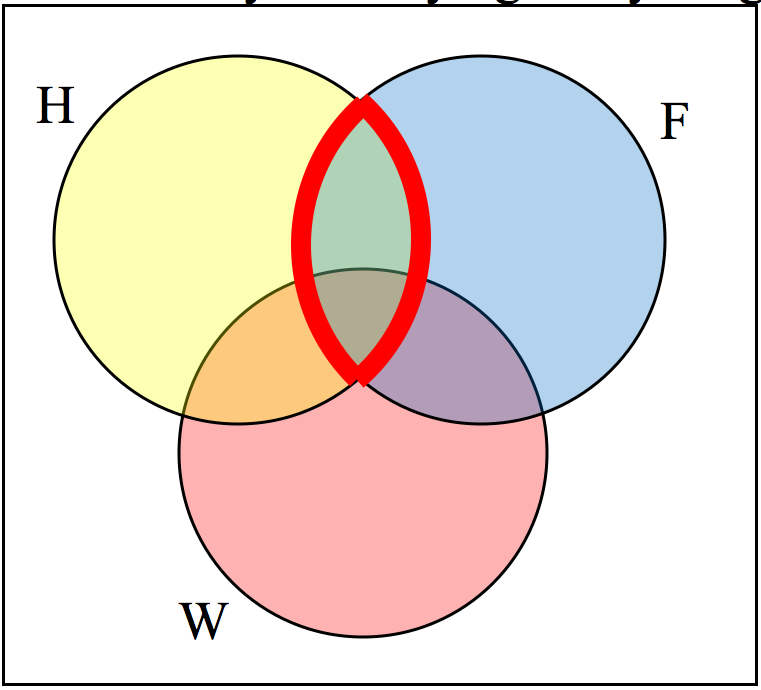
The intersection of H and F

Now, \(\left(H \cap F\right)^C \cap W\) will contain everything not in the set identified above that is also in set \(W\text{.}\)

All elements that are not in both sets H and F, and are in set W.
Example 2.3.4.

Create an expression to represent the outlined part of the Venn diagram shown.

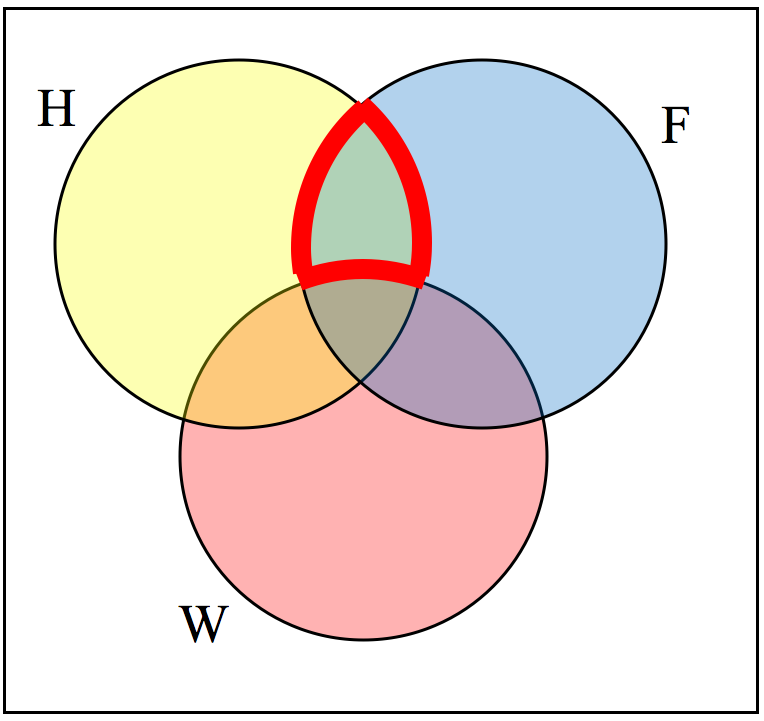
Elements in H and F but not in W
Solution.

The elements in the outlined set are in sets H and F, but are not in set W. So we could represent this set as \(H \cap F \cap W^C\)

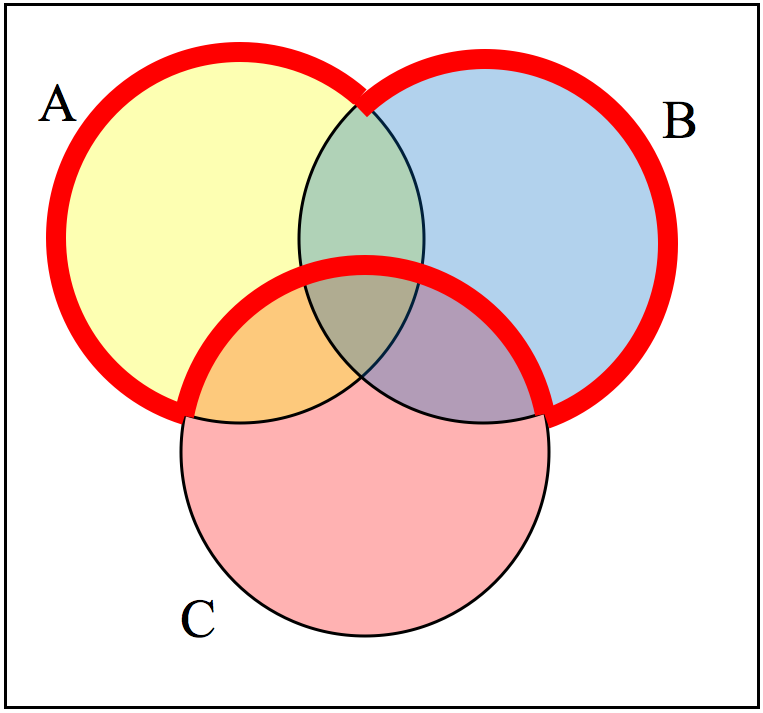
Problem 2.3.5. Try It Now.

Create an expression to represent the outlined portion of the Venn diagram shown.

Elements in A or B but not in C
Answer.
\(A \cup B \cap C^C\)
Problem 2.3.6. Try It Now.

Let \(A = \{1, 2, 3, 4, 5, 6\}\) and \(B = \{2, 4, 6, 8\}\text{.}\)

Find the cardinality of each:

  1. \(\displaystyle B\)

  2. \(\displaystyle A \cup B\)

  3. \(\displaystyle A \cap B\)

Answer.

  1. The cardinality of B is 4, since there are 4 elements in the set.

  2. The cardinality of \(A \cup B\) is 7, since \(A \cup B = \{1, 2, 3, 4, 5, 6, 8\}\text{,}\) which contains 7 elements.

  3. The cardinality of \(A \cap B\) is 3, since \(A \cap B = \{2, 4, 6\}\text{,}\) which contains 3 elements.