Skip to main content

Exercises 7.5 Chapter Test

1.

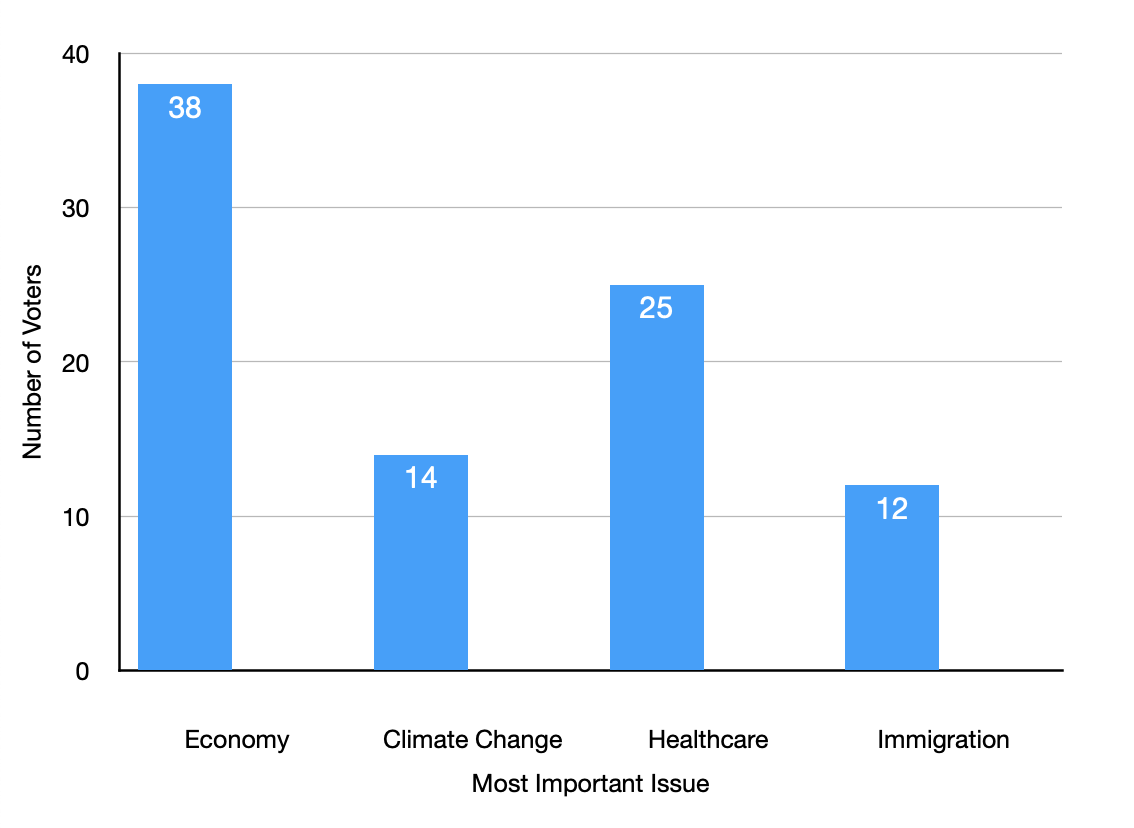
A group of voters was surveyed about the issues that are most important to them. The results are summarized in the table.

Table 7.5.1.
Number of Respondants Most Important Issue
38 Economy
14 Climate Change
25 Healthcare
12 Immigration

  1. How many people were surveyed?

  2. Create a bar graph to display this data.

  3. Create a pie chart to display this data.

Answer.

  1. 89

2.

Scores on a test are given below. Organize this data into class intervals with a width of 5, starting at 30. Create a histogram for the data.

48, 53, 32, 41, 46, 33, 42, 51, 36, 37, 47, 39, 54, 33, 48, 40, 36, 35, 49, 52, 39, 44

Answer.

Table 7.5.2.
Greater than or equal to Less than Frequency
30 35 3
35 40 6
40 45 4
45 50 5
50 55 4
A histogram that corresponds to the frequency table.
Figure 7.5.3. Image Credit: RRCC

3.

For the dataset:

\begin{equation*} \{ 8, 4, 8, 9, 8, 7, 3, 2, 1, 9, 8 \} \end{equation*}

  1. Find mean, median, and mode.

  2. Give the 5-number summary.

  3. Find sample standard deviation.

Answer.

  1. \(\mu = 6.09\text{,}\) \(M = 8\text{,}\) mode \(=8\)

  2. Min = 1, Q1 = 3, Median = 8, Q3 = 8, Max = 9

  3. 2.98

Solution.

  1. The mean is the sum of the values, divided by the number of values:

    \begin{equation*} \mu = \frac{8+4+8+9+8+7+3+2+1+9+8}{11} = \frac{67}{11}=6.09 \end{equation*}

  2. The five-number summary consists of the max, min, median, 1st quartile and 3rd quartile.

    Maximum = 9, Minimum = 1, Median = 8.

    To find the 1st quartile, \(L = 0.25(11) = 2.75\text{.}\) We round up and look at the 3rd value. \(Q_1 = 3\text{.}\)

    To find the 3rd quartile, \(L = 0.75(11) = 8.25\text{.}\) We round up and look at the 9th value. \(Q_3 = 8\text{.}\)

  3. We will added up squared deviations, divide by 10 (\(n - 1\)) and then take the square root of the result.

    Table 7.5.4.
    Frequency \(x\) \(x - \mu\) \((x - \mu)^2\)
    1 1 \(1 - 6.09 = -5.09\) \((-5.09)^2=25.9081\)
    1 2 \(2 - 6.09 = -4.09\) \((-4.09)^2=16.7281\)
    1 3 \(3 - 6.09 = -3.09\) \((-3.09)^2=9.5481\)
    1 4 \(4 - 6.09 = -2.09\) \((-2.09)^2=4.3681\)
    1 7 \(7 - 6.09 = 0.91\) \((0.91)^2=0.8281\)
    4 8 \(8 - 6.09 = 1.91\) \((1.91)^2=3.6481\)
    2 9 \(9 - 6.09 = 2.91\) \((2.91)^2=8.4681\)

    The sum of the squared deviations is:

    \begin{equation*} 25.9081+16.7281+9.5481+4.3681+0.8281+4\cdot 3.6481+2 \cdot 8.4681=88.9091 \end{equation*}

    Divide by \(n-1=10\) and take the square root:

    \begin{equation*} \sqrt{\frac{88.9091}{10}}=2.98 \end{equation*}
4.

The table below gives the heights (in inches) of a women’s basketball team.

Table 7.5.5.
Height Frequency
64 1
65 2
67 3
68 6
69 4
70 5
72 1
73 1

  1. Find the mean height.

  2. Find the median height.

  3. Find the first and third quartile.

  4. Find the population standard deviation.

  5. Create a box-and-whiskers plot.

Answer.

  1. 68.4 inches

  2. 68 inches

  3. \(\displaystyle Q_1 = 67, Q_3 = 70\)

  4. 2.06 inches

  5. See solution.

Solution.

  1. There are \(n = 1+2+3+6+4+5+1+1=23\)values.

    \begin{equation*} \mu = \frac{1\cdot 64 + 2\cdot 65 + 3 \cdot 67 + 6 \cdot 68 + 4 \cdot 69 + 5 \cdot 70 + 1 \cdot 72 + 1 \cdot 73}{23} \end{equation*}
    \begin{equation*} \mu = \frac{1574}{23}=68.4 \end{equation*}

  2. There are \(n = 23\) values. To find the median, \(L = 0.5(23) = 11.5\text{.}\) Round up and look at the 12th value.

    Table 7.5.6.
    Height Frequency Values
    64 1 1
    65 2 2 - 3
    67 3 4 - 6
    68 6 7 - 12
    69 4 13 - 16
    70 5 17 - 21
    72 1 22
    73 1 23

    The 12th value is 68. \(M = 68\text{.}\)

  3. To find the 1st quartile, \(L = 0.25(23)=5.75\text{.}\) Round up and look at the 6th value. \(Q_1 = 67\text{.}\)

    To find the 3rd quartile, \(L = 0.75(23) = 17.25\text{.}\) Round up and look at the 18th value. \(Q_3 = 70\text{.}\)

  4. To find the population standard deviation, add up squared deviations from the mean, divide by the number values in the dataset, and take the square root.

    Table 7.5.7.
    Frequency \(x\) \(x - \mu\) \((x-\mu)^2\)
    1 \(64\) \(64 - 68.4 = -4.4\) \((-4.4)^2 = 19.36\)
    2 \(65\) \(65 - 68.4 = -3.4\) \((-3.4)^2 = 11.56\)
    3 \(67\) \(67 - 68.4 = -1.4\) \((-1.4)^2 = 1.96\)
    6 \(68\) \(68 - 68.4 = -0.4\) \((-0.4)^2 = 0.16\)
    4 \(69\) \(69 - 68.4 = 0.6\) \((0.6)^2 = 0.36\)
    5 \(70\) \(70 - 68.4 = 1.6\) \((1.6)^2 = 2.56\)
    1 \(72\) \(72 - 68.4 = 3.6\) \((3.6)^2 = 12.96\)
    1 \(73\) \(73 - 68.4 = 4.6\) \((4.6)^2 = 21.16\)

    Add up the squared deviations, by multiplyig them by their frequencies:

    \begin{equation*} 1 \cdot 19.36+2\cdot 11.56+3 \cdot 1.96 + 6\cdot 0.16 + 4\cdot 0.36+5\cdot 2.56 + 1\cdot 12.96 + 1 \cdot 21.16 = 97.68 \end{equation*}

    Then divide by \(n = 23\) and take the square root:

    \begin{equation*} \sqrt{\frac{97.68}{23}}=2.06 \end{equation*}
  5. The box will extend from \(Q_1 = 67\) to \(Q_3 = 70\) with a line drawn at the median, \(M = 68\text{.}\) The whiskers extend from the minimum value of \(64\) to the maximum value of \(73\text{.}\)
    The answer to this part of the exercise.
    Figure 7.5.8. Image Credit: RRCC
5.

The box plots below show the ages of both men and women Olympic gymnasts. Use the box plots to answer the following questions.

The female Olympic gymnast box goes from 16 to 19 with whiskers extending from 14 to 24. A line is drawn at 17. The male Olympic gymnast box goes from 21 to 26 with whiskers extending from 16 to 32. A line is drawn at 23.
Figure 7.5.9. Image Credit: RRCC

  1. What is the median age of a female Olympic gymnast?

  2. 25% of the female gymnasts are ___ or older.

  3. ____ % of the male gymnasts are 23 or younger.

  4. Which gender has a larger range in ages of athletes?

Answer.

  1. 17

  2. 16

  3. 50%

  4. Male gymnast ages have a larger range.

6.

The mean price of a dozen eggs is $2.19 with a standard deviation of $0.09. The mean price of a pound of chicken is $5.89 with a standard deviation of $0.15. Which item had more variability in prices? Explain.

Answer.
The eggs have a larger variability in price because they have a larger coefficient of variation.
Solution.

The coefficient of variation for the eggs is:

\begin{equation*} CV = \frac{s}{\mu} \times 100\% = \frac{0.09}{2.19} \times 100\% = 4.1\% \end{equation*}

The coefficient of varation for the chicken is:

\begin{equation*} CV = \frac{0.15}{5.89} \times 100\% = 2.5\% \end{equation*}

Since the coefficient of varation is larger for the eggs, there is more variability in egg prices than chicken.