Skip to main content

Exercises 2.5 Exercises

1.

List out the elements of the set “The letters of the word Mississippi”

Answer.
{m, i, s, p}
2.

List out the elements of the set “Months of the year"

3.

Is \(\{1, 3, 5\}\) a subset of the set of odd integers?

Answer.
Yes
4.

Is \(\{A, B, C\}\) a subset of the set of letters of the alphabet?

Exercise Group.

Consider the sets below and indicate if each statement is true or false.

\(A = \{1, 2, 3, 4, 5\}, B = \{1, 3, 5\}, C = \{4, 6\}, U\) = {numbers from 0 to 10}

5.
\(3 \in B\)
Answer.
True. 3 is an element in set B
6.
\(5 \in C\)
7.
\(B \subset A\)
Answer.
True. All elements in B are also in set A.
8.
\(C \subset A\)
9.
\(C \subset B\)
Answer.
False. The elements in set C are not in set B.
10.
\(C \subset U\)
Exercise Group.

Draw a bag diagram and find the cardinal number of each set.

12.
\(B=\{\{1,2\}, \{1\}\}\)
14.
\(A=\{\{a,b\}, c, d\}\)
16.
\(S = \{ \}\)
17.
List all subsets of \(S=\{ \text{math,history,English}\}\)
Answer.
{ }, {math}, {history}, {English}, {math, history}, {math, English}, {history, English}, {math, history, English}
18.
List all subsets of \(P = \){tea, muffin, cookie}
19.
How many subsets does \(A=\){Colorado, Utah, Wyoming, Montana, Idaho} have?
Answer.
32
20.
How many subsets does \(B = \){lily, daisy, sunflower, rose, iris, daffodil} have? How many of those subsets are proper subsets?
Exercise Group.

Use the sets below to find the following

\(A = \{1, 3, 5, 7\}, B = \{1, 2, 3, 4\}, C = \{5, 7, 9\}, U =\{1, 2, 3, 4, 5, .., 10\}\)

21.
\(A \cup B\)
Answer.
{1, 2, 3, 4, 5, 7}
22.
\(A \cap B\)
24.
\(A \cup C\)
25.
\(B \cup C\)
Answer.
{1, 2, 3, 4, 5, 7, 9}
26.
\(B \cap C\)
27.
\(A^C\)
Answer.
{2, 4, 6, 8, 9, 10}
28.
\(B^C\)
30.
\(A^C \cup B\)
Exercise Group.

Let D = {b, a, c, k}, E = {t, a, s, k}, F = {b, a, t, h}. Using these sets, find the following:

32.
\(F^C \cap D\)
33.
\(\left( D \cap E \right) \cup F\)
Answer.
{a, k, b, t, h}
34.
\(D \cap \left(E \cup F \right)\)
35.
\(\left(F \cap E\right)^C \cap D\)
Answer.
{b, c, k}
36.
\(\left( D \cup E \right)^C \cap F\)
Exercise Group.

Create a Venn diagram to illustrate each of the following:

37.
\(A \cap B^C\)
38.
\(A \cup B^C\)
39.
\(\left(F \cap E \right) \cup D\)
40.
\(\left(D \cup E \right)^C \cap F\)
41.
\(\left(F^C \cap E^C \right) \cap D\)
42.
\(\left(D \cup E \right) \cup F\)
Exercise Group.

Write an expression for each shaded region.

43.
The shaded region includes where B overlaps with either A or C.
Answer.
One possible answer: \(\left(A\cap B\right)\cup\left(B\cap C\right)\)
44.
The shaded region includes the part of set B that does not overlap with any other sets (A or C).
45.
The shaded region include all of set C, as well as the part of set A that does not overlap with set B.
Answer.
\(\left(A \cap B^C\right)\cup C\)
46.
The shaded region includes everything in sets A and B, as well as parts of set A or B that do not overlap with set C.
Exercise Group.

The Venn diagram here shows the cardinality of each set. Use this to find the cardinality of each set.

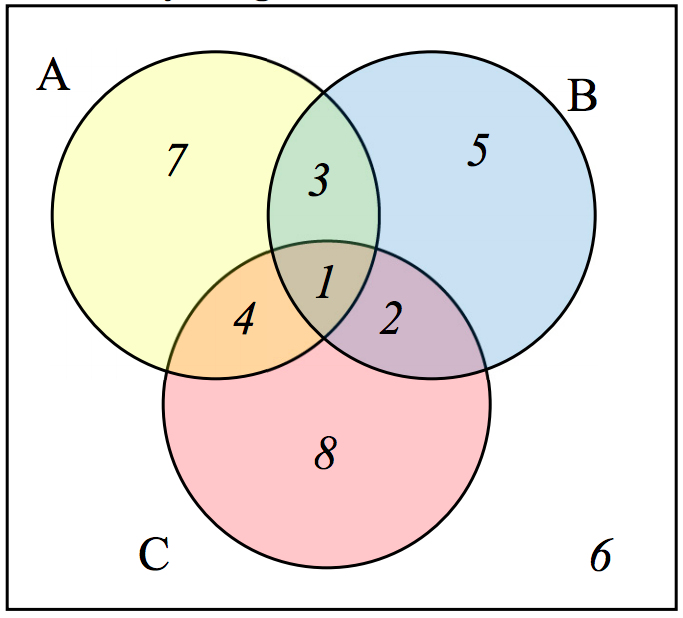
Numbers in the Venn diagram are: only A = 7; only A and B = 3; only B = 5; A, B, and C = 1; only A and C = 4; only B and C = 2; only C = 8; outside all sets = 6
48.
\(n\left(B\right)\)
49.
\(\left(A \cap C\right)\)
Answer.
5
50.
\(n\left(B \cup C\right)\)
51.
\(n\left(A \cap B \cap C^C \right)\)
Answer.
3
52.
\(n\left(A \cap B^C \cap C\right)\)
Exercise Group.

Let \(A = \{1, 2, 3, 4, 5\}, B = \{1, 3, 4\}, \text{and }C = \{4, 6\}\)

Find the cardinality of the given sets.

54.
\(n(B)\)
56.
\(n(A \cap C)\)
57.
If \(n(G)=20, n(H)=30, n(G \cap H)=5\text{,}\) find \(n(G \cup H)\text{.}\)
Answer.
45
58.
If \(n(G) = 5, n(H) = 8, n(G \cap H) = 4\text{,}\) find \(n(G \cup H)\text{,}\)
59.

A survey was given asking whether they watch movies at home from Netflix, Redbox, or a video store. Use the results to determine how many people use Redbox.

  • 52 only use Netflix

  • 24 only use a video store

  • 62 only use Redbox

  • 16 use only a video store and Redbox

  • 48 use only Netflix and Redbox

  • 30 use only a video store and Netflix

  • 10 use all three

  • 25 use none of these

Answer.
136
60.

A survey asked buyers whether color, size, or brand influenced their choice of cell phone. The results are below. How many people were influenced by brand?

  • 5 said only color

  • 8 only said size

  • 16 only said brand

  • 20 said only color and size

  • 42 said only color and brand

  • 53 said only size and brand

  • 102 said all three

  • 20 said none of these

61.

Use the given information to complete a Venn diagram, then determine: a) how many students have seen exactly one of these movies, and b) how many had seen only Star Wars.

  • 18 had seen The Matrix

  • 24 had seen Star Wars

  • 20 had seen Lord of the Rings

  • 10 had seen the Matrix and Star Wars

  • 14 had seen Lord of the Rings and Star Wars

  • 12 had seen the Matrix and Lord of the Rings

  • 6 had seen all three

Answer.
a) 8 b) 6
62.

A survey asked people what alternative transportation modes they use. Using the data to complete a Venn diagram, then determine: a) what percent of people only ride the bus, and b) how many people don’t use any alternate transportation.

  • 30% use the bus

  • 20% ride a bicycle

  • 25% walk

  • 5% use the bus and ride a bicycle

  • 10% ride a bicycle and walk

  • 12% use the bus and walk

  • 2% use all three

63.

A group of students was surveyed about the student services they use. The results are summarized below.

  • 6 use the rec center, library, and computer labs

  • 16 use the rec center and library

  • 28 use the library

  • 14 use the library and computer labs

  • 9 use the rec center and computer labs, but not library

  • 23 use the rec center, but not library

  • 18 were using only computer labs

  • 37 were using none of these services

  1. How many students were surveyed?

  2. How many students were using only the rec center?

  3. How many students were using computer labs?

Answer.

  1. 106

  2. 14

  3. 41

64.

A survey is taken of one hundred people who vacationed at a resort. The following information was obtained,

  • 17 took tennis lesson, attended the Saturday night barbecue, and rented a surfboard

  • 28 attended the barbecue and rented a surfboard

  • 24 took tennis lessons and rented a surfboard

  • 42 took tennis lessons, but didn't attend the barbecue

  • 86 took tennis lessons or rented a surfboard

  • 14 only rented a surfboard

  • 14 did none of these things

  1. How many attended the barbecue?

  2. How many rented a surfboard?

65.

A survey was made of 200 city residents to study the use of mass transit facilities. According to the survey:

  • 83 did not use mass transit

  • 68 used the train

  • 44 only used the subway

  • 59 used the bus

Explain how you can use this information to deduce that some residents must use both the bus and train.