Section 5 The Torque Problem
In this final section we are going to put together what we have worked through so far to take a look at an important application of vectors, torque.
Definition 5.1.
Torque is a vector that is the moment of force that that tends to cause rotation.Suppose that we have a socket wrench to tighten a bolt. The action of turning this wrench will create a tendency to get the bolt to turn. When we turn the wrench one way, the bolt will losen, when we turn the wrench the other way the bolt will tighten. The force that gives us this tendancy is called torque and it is a vector that we can compute using the length of the wrench and the force that we will apply to the wrench.
To manage this computation, we are going to need to make a force diagram with the wrench as one vector and the force applied as the other vector. Here is an example of what that diagram will look like,
or
Now to compute the torque, we are going to cross the "wrench vector" with the force vector. This will give us a vector pointing into or out of the page. These direction will tell us if the force will turn into or out of the page. In math that is,
Example 5.4. Torque Example.
A bolt is tightened by applying a 40 N force to a 0.25 m wrench. The force is applied orthogonal to the wrench. Find the torque and its magnitude.
If we are going to use the cross product, we are going to need to make the included information into vector. Lets start with the wrench.
Making the wrench a vectorJust as it is in the above figure, let's assume that the wrench is on the x-axis. This will make it easier to work with and encode in a vector. We have been given that the wrench is 0.25 m long, so we know that this will need to be the length (magnitude) of the vector. Additionally, we have the vector on the \(x \) - axis, so there should be a 0 for the \(y \) component of the vector and a 0 for the \(z \) component . These thoughs should give us,
The next thing that we need to do is make the give 40 N into a vector encoded in our diagram. Since we know that the force is being applied orthogonal to the wrench, we can use the \(\mathbf{j} = \langle 0 ,1 \rangle \) as a building block. With this vector in hand, we will scale it using the given 40 N to get a vector that is the correct length, and the choice to use \(\mathbf{j} \) will give us the correct direction.
Looking at the resulting vector (the torque vector) we can see that it is infact pointing out of the page. If on the other hand the force had been the other direction, we would have had a torque pointing into the page.
Finally we can find the magnitude of this vector using the equation that we considered earler.
Checkpoint 5.6.
Checkpoint 5.7.
Checkpoint 5.8.
The final question that we are going to consider is how we will compute the torque if the force is not orthogonal. For this we are going to need to use the equation for a unit vector that developed earler, \(\textbf{u} = \langle \cos(\theta) , \sin(\theta) \rangle \) as well as the dot product.
Example 5.9.
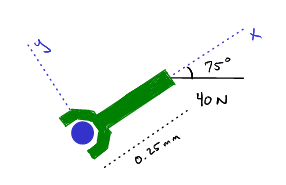
Let's suppose that we have a wrench that is .45 m long and the 40 N force is being applied at an angle \(75^{\circ} \) to the wrench as in the figure.
To start we are will need to