Overview of Matrices

Subsection 3.1 Compatibility

Unlike addition, the check will have to do with the columns of the matrix on the left in the product, and the number of rows in the matrix on the right in the product. Let's break this down a bit more. Consider,

Now if we wanted to find \(AB \) we would need to check to make sure that this product is possible. To do this we observe in the expression \(AB \text{,}\) matrix \(A \) is "left" in the written description in of the product. So we will note the number of columns that is has (in this case 2). The we observe that \(B \) is "right" in the written description in of the product. So we will note the number of rows that is has (in this case 2). Since these two match, we say that the two matrices are compatible for matrix multiplication with \(A \) on the left and \(B \) on the right.

This compatibility check is really important when working with matrices. In machine learning, the weight matrices often need to interact with another through matrix multiplication. So keeping an eye on the matrix size info is a must as the matrices are designed and utilized.

Let's take a look at how Python reports a compatibility problem. (Hint, this will look a lot like what we saw in the last Python code-block example.)

# Include the numpy module. 
import numpy as np

# Assign matrix A and matrix B from Checkpoint 3.1
A  = np.array([[1, 2, 2], [0, 5, 1], [2, -9 , 3]])
B  = np.array([[0,-2, 8], [10, -2, -4]])

# Compute the product BA and assign it to C
C = np.dot(B, A)

# This will print C. (The product BA)
print(C)

# Try to compute the product AB
D = np.dot(A, B)

# This would print D if it could be computed. 
print(D)

The output of the above code gives us this:

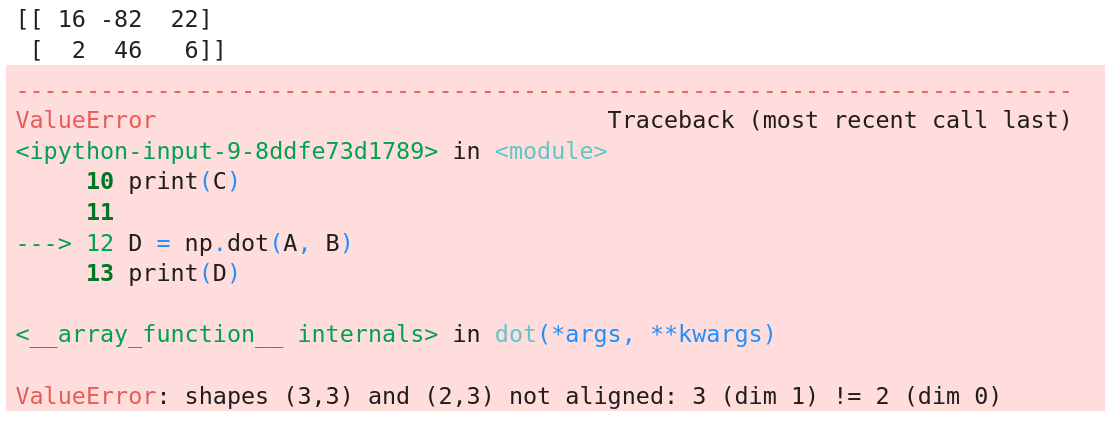
Since the product that does work we printed before the incompatible product, we can see the printed product, and then the error. At this point take a close look at the error here. Once again this is a good error to key in on, as it is something that will come up if there are shape (dimension) alignment issues.

Subsection 3.2 The Algorithm

Up to this point we have talked about the vocab of matrix multiplication as well as how to check if it can be preformed. Now let's explore how the product is computed. Let's consider again the matrices,

Above we stated that \(AB \) can be computed, and we did the column = row compatibility check. Now we will showcase how this product is computed. To preform the product \(AB \) , we are going to use the dot product on the columns of \(A \) and the rows of \(B \text{.}\)

So, to find \(AB \) given,

we will dot row 1 of \(A \) with all the columns of \(B \text{.}\) The fact that we are using row 1 of \(A \) means that we will be computing the first row in the product matrix. When we switch to row 2 of \(A \) we will be computed the second row of the product matrix, and so on.

So,

Throughout all of this we need to be thinking, "row by column".

# Include the numpy module. 
import numpy as np

# Assign matrix C and matrix D from Checkpoint 3.3
C  = np.array([[9, 1], [2, -4], [2, 7]])
D  = np.array([[0, 1, 3], [1, -2, 6]])

# Compute the product of C and D and assign it to M
M = np.dot(C, D)

# This will print M
print(M)

Notice: The syntax to multiply matrices is np.dot(A,B) not *. As we will see in the next section, the * is for a different operation. Also, the order that they appear in the parenthesizes (from left to right) is the order of the product.

Subsection 3.3 The Hadamard Product

We started this section by indicating that matrix multiplication does not have the entry by entry process that we see with matrix addition. It should be noted that there is, in fact, another product that does work this way.

This product should be thought of as an entirely different operation to matrix multiplication. With that in mind, the compatibility check for the Hadamard product is that the two matrices in the product must have be the same size (same number of rows and columns).